Calling on @Jan @Richard @amelia @bpinaud @melancon: we have cleared a bit of a milestone with this paper, and I think it is time we all meet again.
This is now done. In fact, I think I have done one better: thanks to the progress made by Bruno and Guy, I was able to finish section 5, and write section 6.1, of the paper. This means that all four techniques are now described and their result quantified (section 5). They are also compared against each other in a qualitative way. Section 6.2 is going to quantify the extent to which pairs of techniques converge to the same results; I will draft after Bruno has finished the computation.
Section 6.1 contains also a summary discussion in the form of Table 3 and Figure 5. Figure 5 is what you want (see below). The graphic stuff is coarse, we’ll polish it but I am prioritizing speed so we can have this discussion with you.
I suggest you read sections 5 and 6.1, then we have a discussion and you (Jan, Amelia, Richard) tell us what you see in these reduced networks, and well they satisfy you. I suggest Wednesday 17th (will be on the road on Thur and Fri).
Bruno, Guy, I also finally have some kind of answer to:
Yes. k is a granularity parameter. If you set it to a value k*, that value becomes the maximum possible redundancy that any edge can have. This is because redundancy is the numerosity of the union between the k strongest-tied neighbors of ego, and the k* strongest-tied neighbors of alter. At the very maximum, these can be… k*: complete overlap. So, if you remove all edges with redundancy < k* and your network is still too large, you can recompute redundancy usign a higher value for k. However, there is a catch: as you reduce more, your giant component dissolves into a number of dense connected components, making your reduction quite meaningless. So, in practice, I think it is not that important how you set your k.
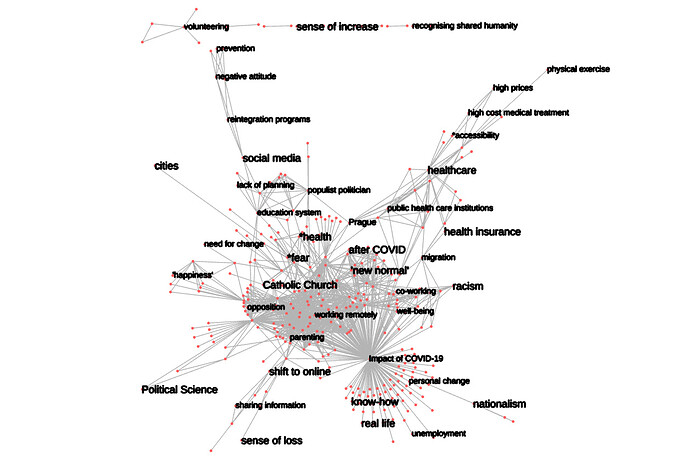
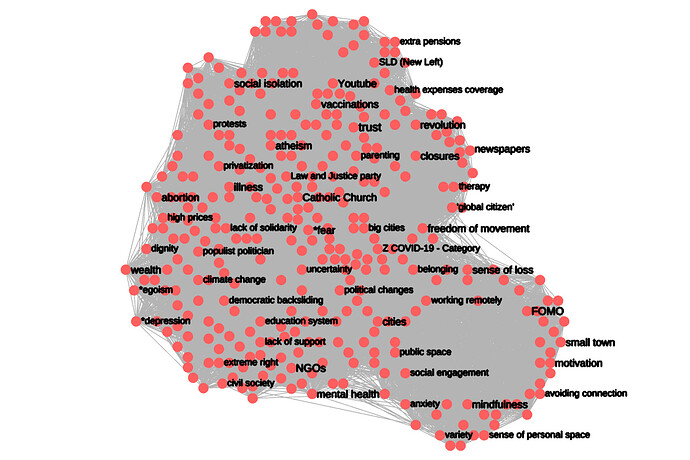
Here is POPREBEL reduced:
By association depth > 8
By association breadth > 2
By highest core values > 63 (highest possible for this dataset)
By Simmelian backbone, redundancy > 5: