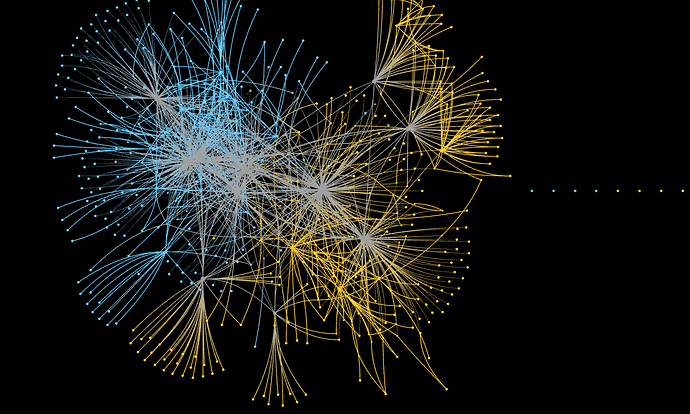
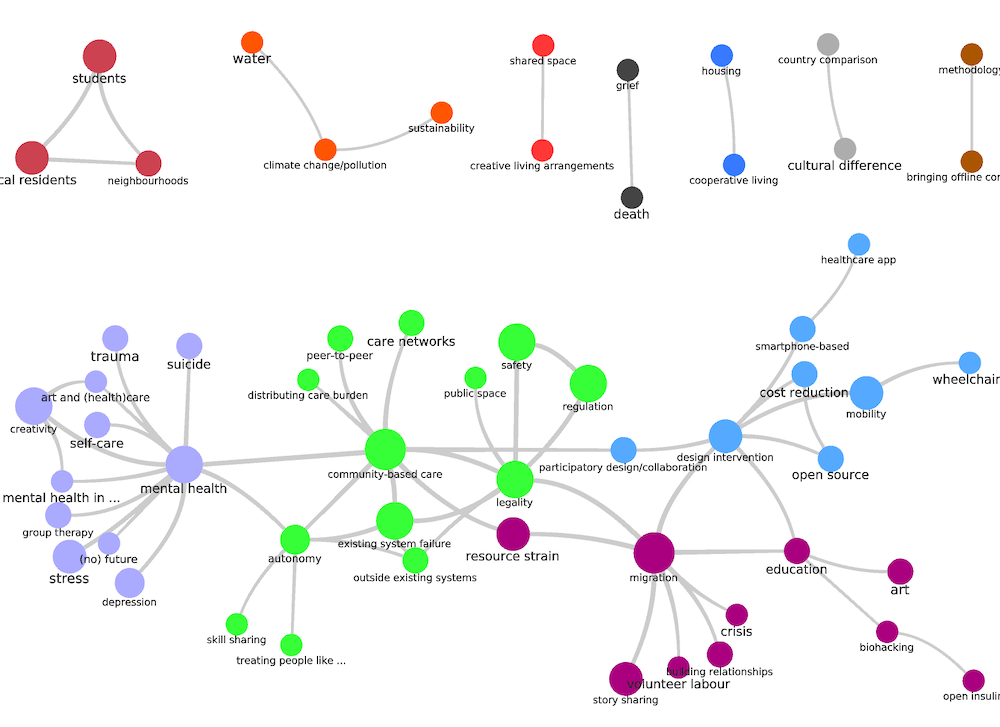
Working on the SSNA white paper has given me the opportunity to sit with the data from three different projects (OpenCare, POPREBEL, NGI Forward) and look for emerging patterns and regularities as I apply various techniques. In the last week I have worked on network reduction. The (social) interaction networks of SSNA projects are usually small and low-density enough that visual inspection reveals a lot about them. This, for example is the joint interaction network of both POPREBEL (yellow) and NGI Forward:
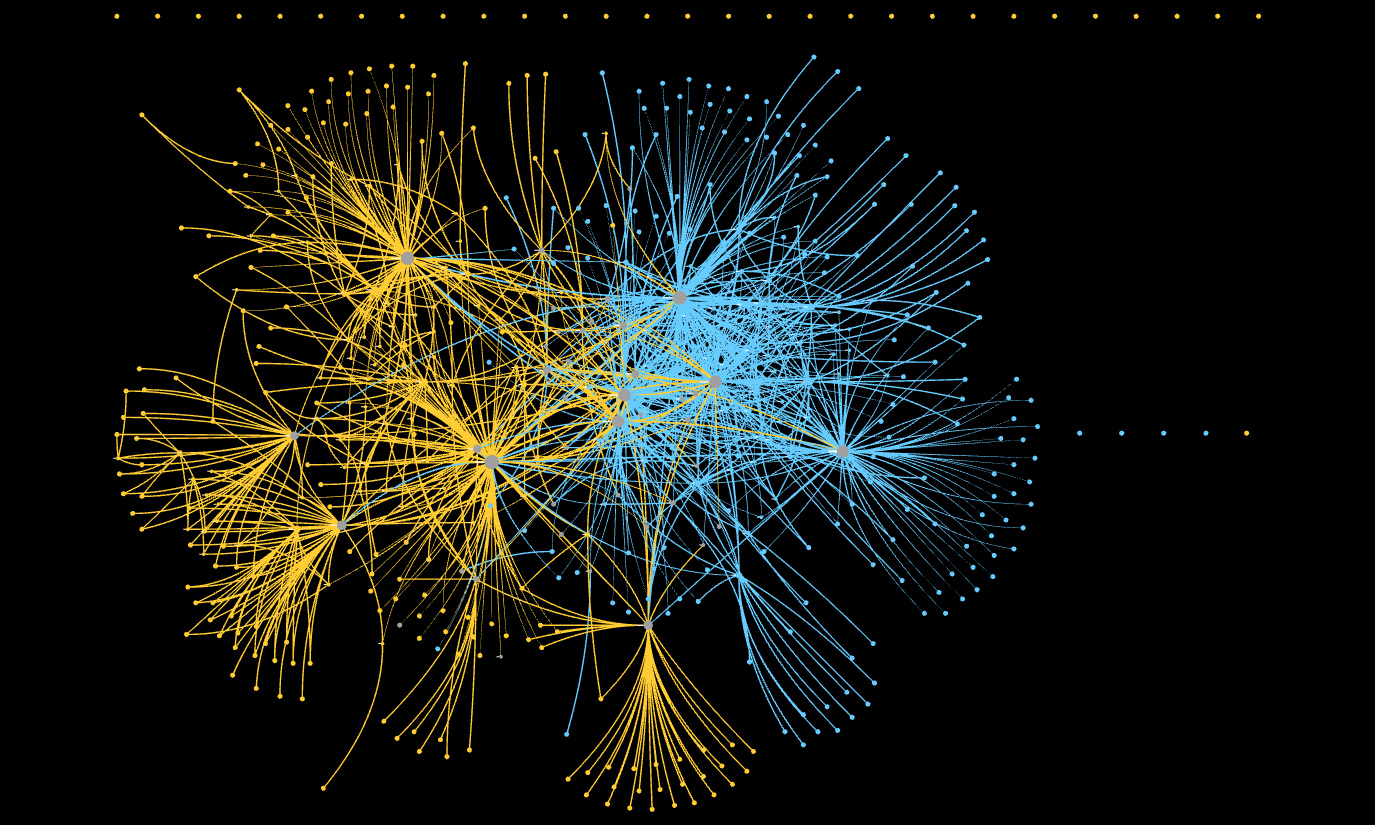
The human eye can immediately make sense of it. Notice how neatly they resolve into the two subnetworks, while the respective communities are still in contact via the people who participate in both discussions (gray nodes). This is a nice result in itself, wonder if @melancon and @brenoust have some comment to make!
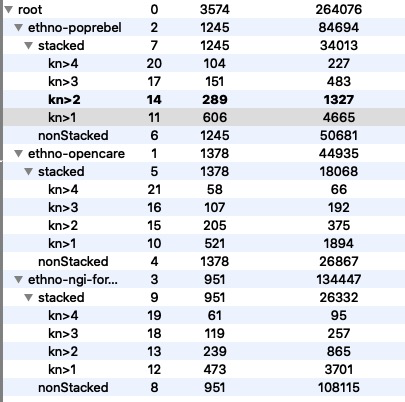
The situation is different for the codes co-occurrence networks. These are very dense by construction: if a single post is annotated with 20 codes, it gives rise to a 20-clique between all these codes. This means adding 20 x 19 / 2 = 190 edges. And it is just one post! This is why, in Graphryder, we need a good filtering utility. Traditionally, we filter by count of co-occurrencies. This is fairly effective… but really, the effectiveness depends on the intensity and style of coding. The more annotations there are, and the more coherent the ontology of codes (which reduces the number of nodes via merge), the denser the graphs become.
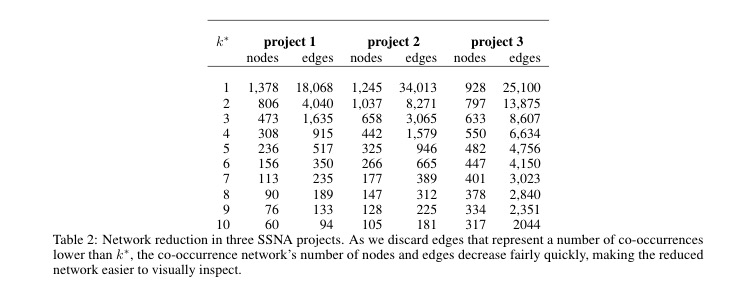
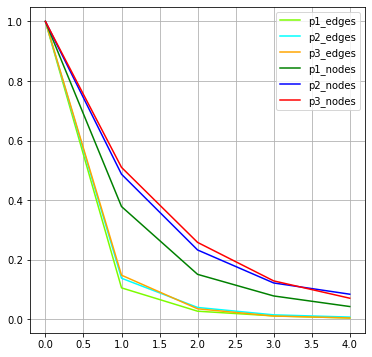
For OpenCare (project 1), discarding edges with k=1 already reduces the edges by almost 80%. But for NGI Forward, with a tighter coding practice, that reduction is less than 50%.
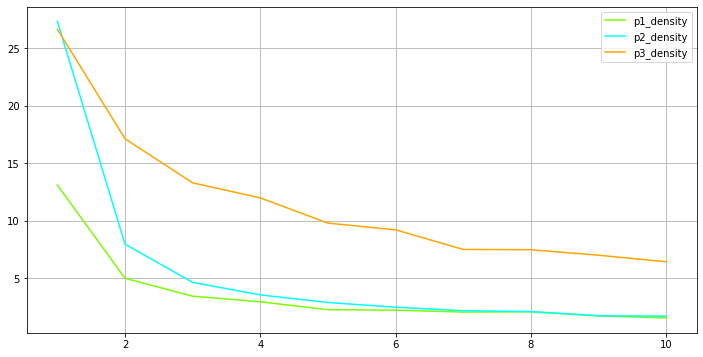
Reduction is effective for low values of k, then it tends to plateau. Nodes decrease slower than edges, and there are differences across projects. A visual representation of this:
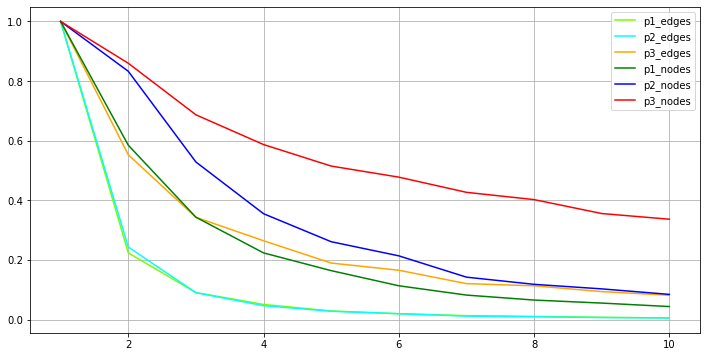
Density (number of edges divided by number of nodes) also decreases. Guy has a paper somewhere arguing that humans process best networks with density lower than 4.
So, I decided to explore a different reduction technique. The reduction implemented in Graphryder, based on k, is a sort “one post one vote” mechanism. Given an edge e, k(e) is the number of post associating the codes connected to each other by e. Now, let kp(e) be the number of authors of the posts that have made that association. What would reduction based on kp(e) look like? And what does it mean?
What it means is “one person one vote”. Suppose Alice has authored one post where code1 and code2 both co-occur. Suppose Bob has authored another one. Call e the edge code1, code2. Now
k(e) = 2
kp(e) = 2
Now suppose Alice believes code1 and code2 to be really important, and deeply connected. She writes five more posts where she makes the same association. Now
k(e) = 6
kp(e) = 2
Alice only gets one vote on e. Additional posts by her will not further change kp(e). The only way that kp(e) can go up is if someone else, say Chris, writes a post that also associates code1 and code2. From a social theory perspective, the main disadvantage of this method is that it loses the information about how important the connection is in the world view of each individual contributor.
However, there are merits in the special case of a reduction by dropping all edges where kp(e) = 1 . In this case, any connection that has been brought up by a single participant in the corpus disappears as a one-off, even if it resurfaces in several contributions of that participant. This seems to be consistent with the way we think about “collective intelligence”.
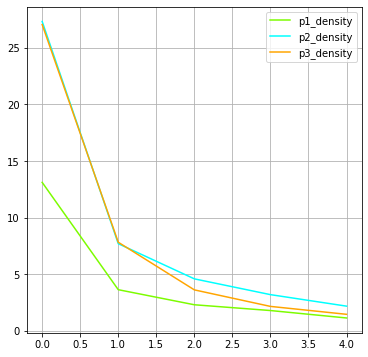
Since, by definition, kp(e) <= k(e), reducing the network based on the values of the former is more effective than on the basis of the value of the latter. Now, for all three projects, 90% of the edges are discarded just by moving kp from 1 to 2.

Density also drops faster:
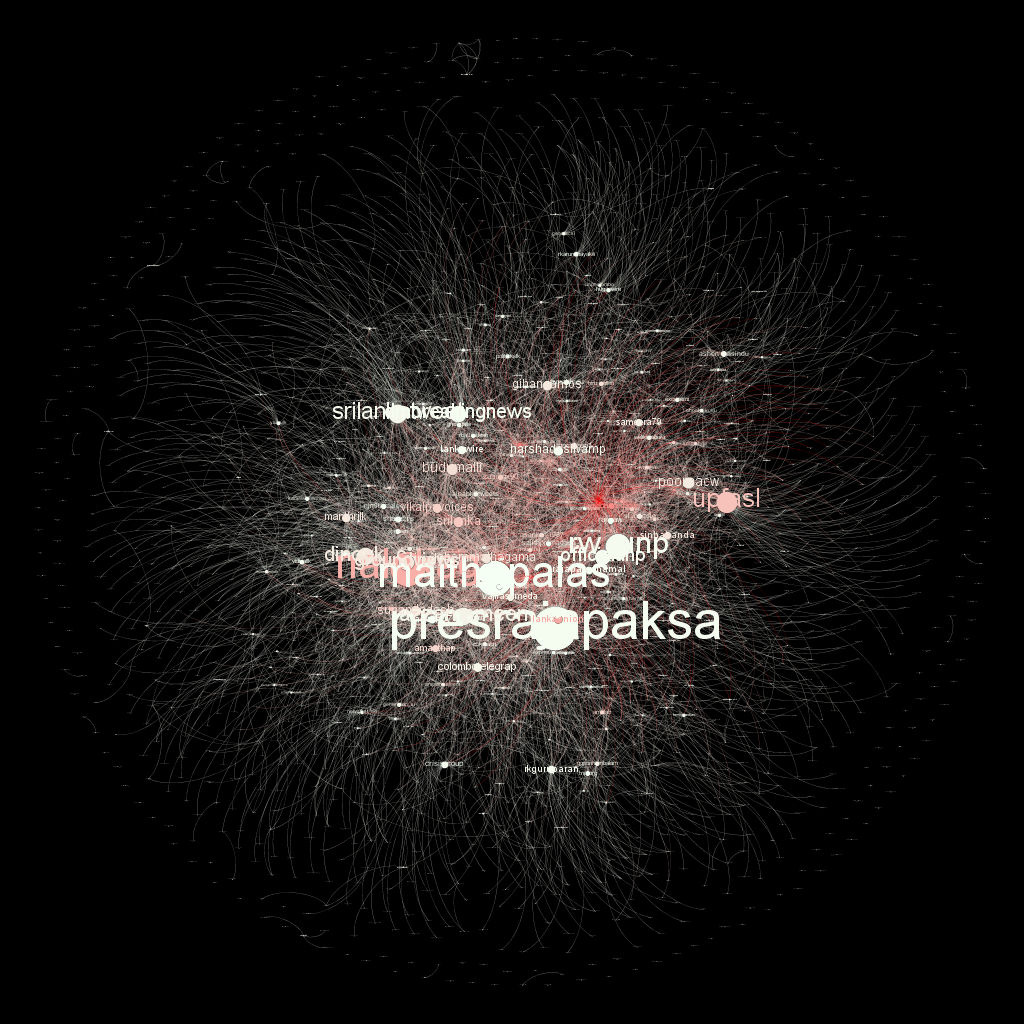
It is worth noting that the correlation between k(e) and kp(e)is positive, but weaker than I expected: less than 0.3 for our whole dataset. This means that the two reduction methods emphasize (in part) different connections. Below, you can admire the codes co-occurrence networks of POPREBEL, already filtered by kp(e) > 1. Redder edges denote higher number of co-occurrences. In case you are wondering, that bright red cluster contains healthcare, low quality, medical treatment, Prague etc.

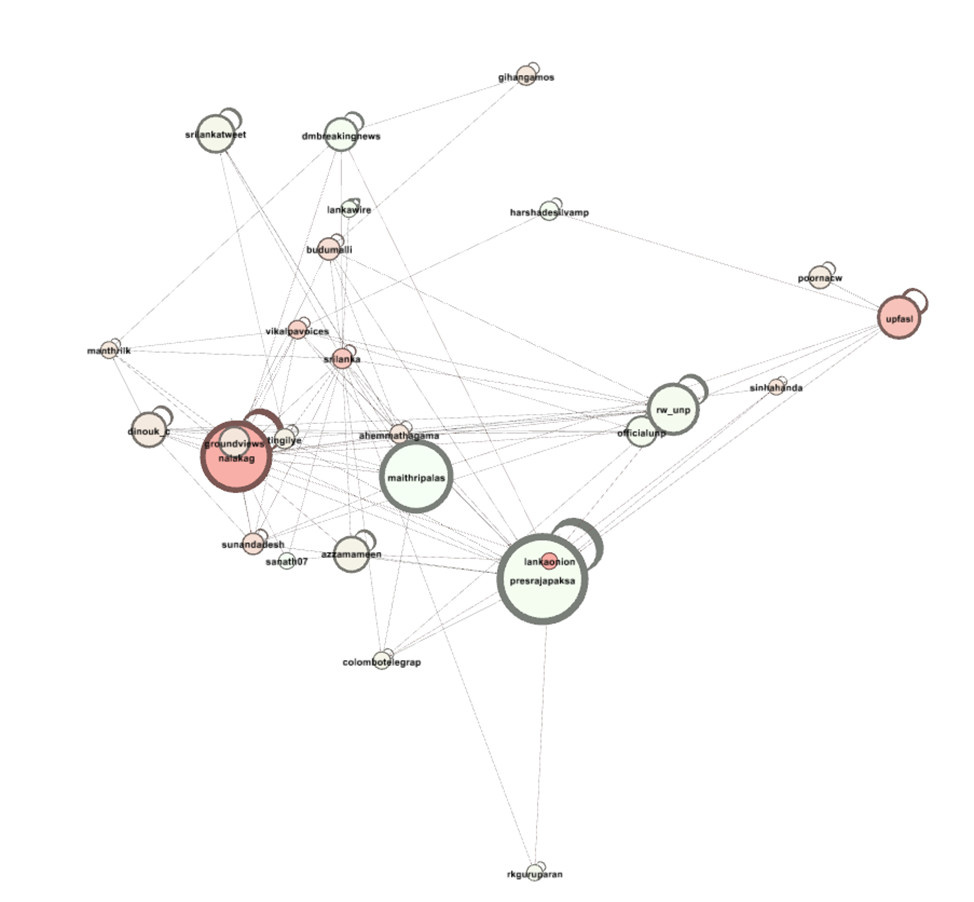
Here is what happens if we color-code for kp(e):

Quite a difference! The bright constellation at the center links codes like Law and Justice Party, big cities, inadequate income, social benefits, and low quality of the health care system.
In general, as so often in data science, there is no “best” (Dutch “allerbeste”) method. The preferred reduction method depends on what you are interested in.
@amelia, @jan, @Richard, @Jirka_Kocian, @Leonie, @katejsim, @Wolha: I would welcome your thoughts on how well “one post one vote” and “one person one vote” mesh with the ethnographer’s research ethos.
The good news is that I have already implemented the code to compute kp(e) when stacking the codes co-occurrence network.