Should we split interviews in several posts, or keep them in one single post?

[alberto]

1. Understanding the problem

The SSNA methodology is in principle compatible with any type of ethnographic data, but it was born in the context of what some call netnography, where the corpus consists in dialogic interaction on an online forum. On a forum, each post is a natural unit of discourse contributed by an informant, and we have coded each post as a whole.

When data come to Open Ethnographer in the form of a transcription of an interview, however, there is a methodological choice to make. This is because our main tool of analysis, the codes co-occurrence network, will look very different depending on the number of codes associated to each contribution, which in turn depends on the length of the contribution itself. Because of how we construct our networks, all codes that co-occur in a contribution form a complete network, also called a clique. Cliques are very dense networks. In our case (CCNs are undirected, meaning that (code1, code2) is the same edge as (code2, code1), and no loops are allowed. This means that the number of edges in a clique with n nodes is n x (n-1) / 2. Another way of looking at it is that the number of edges grows proportionally to the square of the number of codes.

These considerations are important when you are dealing with long interview transcripts. The extent to which you decide to break it into separate contribution implies profound changes to topology of the codes co-occurrence network (CCN). The CCN emerges from the superposition of the various cliques generated by coding the various contributions in the corpus. So, the more pieces you break the transcript into, the less connected the CCN will be. The number of nodes (the codes) stays the same, no matter how you decide to break down your transcript.

2. A toy example

Let’s see a visual example:

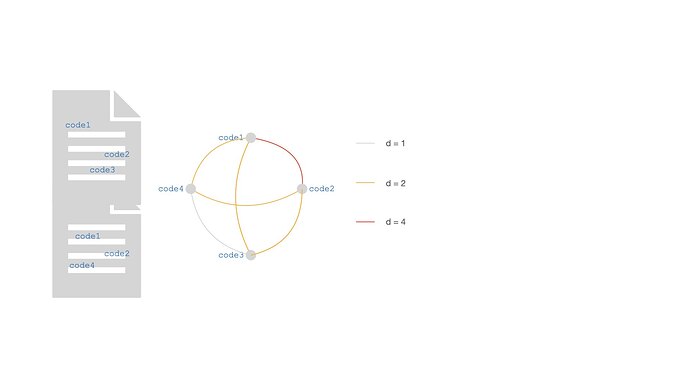
Here, an unbroken interview transcript is coded with four codes, code1 to code4. code1 and code2 appear twice each. The CCN is a complete network (number of edges: 4 x (4-1) / 2 = 6, where each code is connected to each other. The association depth d of each co-occurrence edge is computed by counting the instances of the two codes incident to the edge, and multiplying them together. For example, take the edge code2, code4. code2 appears twice: each instance has a connection with the single instance of code4, so the d(code2, code4) = 2. If you take the edge code1, code2, both codes appear twice: so, the association depth is given by counting the connections of the two instances of code1 with the first instance of code2 (2), plus the connections of the two instances of code1 with the second instance of code2 (also 2). So, d(code1, code2) = 4, which corresponds to 2 x 2.

So, by construction, whenever you code a single unbroken contribution (an interview, a post, whatever) with N codes(leti_cbe the number of occurrences of the codei`), you:

1. generate an N-clique, with N x (N - 1) /2 edges.
2. the association depth d of the edge between any two codes i and j is equal to

d(i,j) = i_c x j_c

Conclusion: if you are coding one single contribution, there is no point inducing a network! You can arrive at the same conclusion simply counting the occurrence of codes. SSNA is designed for collective intelligence, so for a situation in which the contributions are many.

Here is what happens when we break the interview transcript into two:

Each fragment gives rise to complete networks. The overall CCN of the transcript is given by the sum (not the multiplication!) of the CCNs of the individual fragments. As a result, code3 and code4 are no longer connected, because they no longer co-occur on any fragment. Also, only one edge, (code1, code2) has d > 1.

3. An example from POPREBEL: coding an unbroken interview

Let’s try an example with POPREBEL data, as requested by @Wojt. We are going to be looking at the same interview, once in the form of a thread, with each question and each answer in its own separate post (see), and once as a whole post (see). These data are not exactly the same, though, because I found 187 annotations in the former and 88 in the latter.

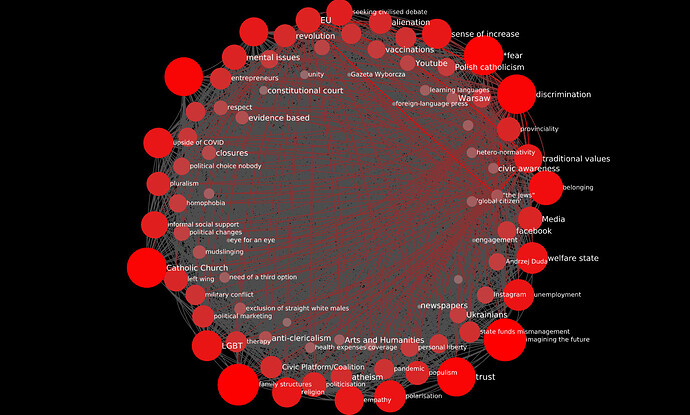
Below you can see the undivided transcript’s CCN. It has 84 codes and 3,486 edges (an 84-clique has 84 x 83 / 2 = 3,486 edges). Redder edges correspond to higher values of d.

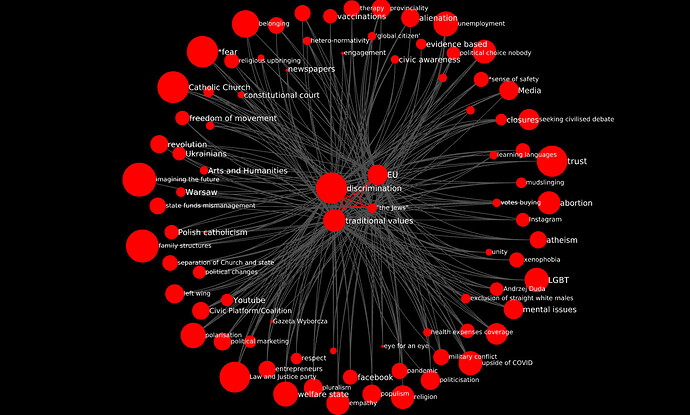
To disentangle this “hairball” network, it makes sense to filter it for higher levels of d. There’s not much granularity, the maximum value of d is 4, and there are only 6 edges where d > = 3. However, filtering for d >= 2 reveals some structure:

All codes connect to one or more of four central codes, which are all connected to each other by high-d edges: discrimination, EU, "the Jews" and traditional values. However, this is purely a mathematical artifact. It simply means that each of these for codes occurs twice, so, by construction, they co-occur four times with one another, and twice with all the other 80 codes, which occur only once.

4. An example from POREBEL: coding an interview broken down into questions and answers

If we induce the CCN from the interview as a topic, we get a network with 130 codes and 569 edges. It has a lot more structure:

Notice the two “islands” on the right: they correspond to individual posts (answers to questions) where the informant obviously “moved on”. These answers do not share one single code with the others. This seems to support the idea that breaking down the transcript in this way is consistent with the sequential way in which this informant was sharing her insights.

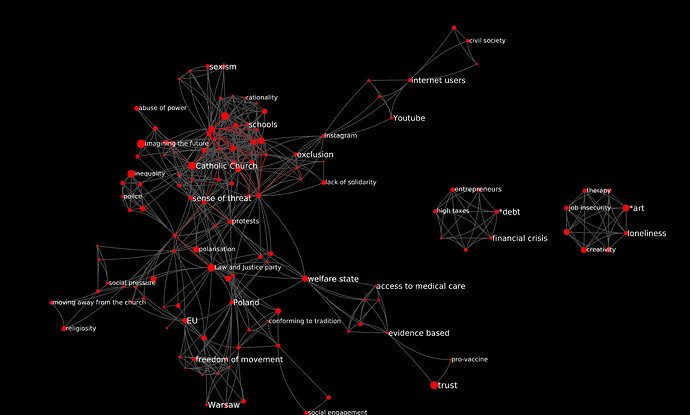
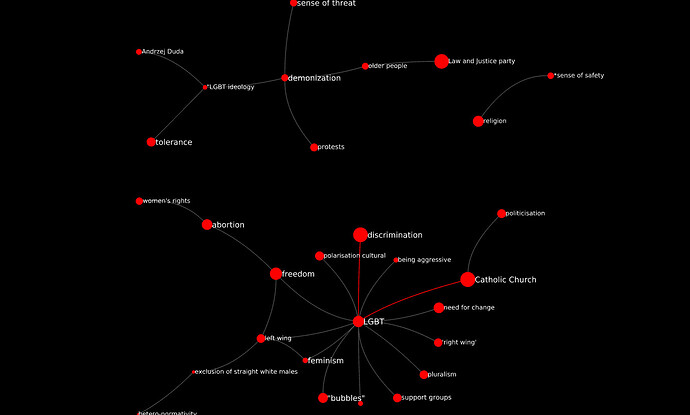
The maximum value of d here is 3, with only three edges having d = 3. If we filter for d >= 2, we get this:

These are three separate islands of codes. LGBT is at the center of the largest one. the two strongest edges in the graph connect it to Catholic Church and discrimination. The latter is the only code that also appears in the central structure of the CCN described in section 3.

5. Conclusions

1. When coding a single contribution, it does not make sense to go through the trouble of inducing a network. Just count the occurrence of codes, and work with the idea that the ones that occur most often are most top-of-mind in the informant.
2. When coding multiple contributions, the size of the contributions is going to affect the shape of the network. Long contributions with many codes give rise to dense networks, and high-d edges that arise as an effect of the multiplicative nature of d.
3. When coding multiple contributions of different sizes, the longer ones will “dominate”: they give rise to potentially many high-d edges. Filtering for high values of d might then result to the researcher looking at networks that only reflect the coding of one or a few very long pieces. This can be mitigated by using metrics different from d.

@rebelethno: what do you think?

[Jan]

WOW! This is exciting. Many thanks Alberto. I teach today the whole day - but tomorrow will get up earlier than planned to study this.

Ciao,

Jan

[Nica]

I have to/will think about it more as I get more familiar with the Graphryder (by the way, @alberto could you please send me the recording from the Zoom walk-through on Monday?) – but my initial sense is, as @Alberto says, the broken-up option is more faithful representationally to how an ethnographic informant shares their thoughts and insights. On the other hand, the unbroken interview is more “classic” in terms of anthropological holistic treatment of whatever body of information it is working with.

To use classic anthropological terminology, the “broken” variant seems more emic structurally/experientially, while the “unbroken” variant is more etic, as it allows insight into the data from a vantage point that is not inhabited by, and maybe not even accessible to, the ethnographic subject who is going to have a sequential experience of the conversation, and a selective rather than comprehensive memory of speaking to the interviewer,

[alberto]

@Nica

To use classic anthropological terminology, the “broken” variant seems more emic structurally/experientially, while the “unbroken” variant is more etic, as it allows insight into the data from a vantage point that is not inhabited by, and maybe not even accessible to, the ethnographic subject who is going to have a sequential experience of the conversation, and a selective rather than comprehensive memory of speaking to the interviewer,

Thanks @Nica. These insights, where we map from (ethnographic) methological choices to mathematical structure, are valuable in our quest to make qualitative research more transparent and accountable.

@alberto

These data are not exactly the same, though, because I found 187 annotations in the former and 88 in the latter.

This is a bit of a shame, as an exact comparison would have been cleaner (though the result about the consequences of unbroken transcript vs. broken by questions and answers is going to be the same). I suppose this happened because, since @Wojt dreamed up the experiment, the team kept coding the broken-up thread. Specifically, you can see that, in the broken-up thread, the questions are often coded: Wojt made a nice argument for when and how to do that.

The difference is not small. The broken up thread has 130 codes (not counting the parent codes of codes atually used in the annotations), whereas the unbroken transcript only has 88.

[Wojt]

Ok, I will try to recreate the “original” coding in a copy of the “broken” interview. Should be ready in a few hours. We may try comparing them then, what do you say?

[Maniamana]

This is super interesting and actually I was wondering, it remind me a lot about what I was doing in my other ethnographic project using SNA. Can we perhaps do it both ways, because why not? It is a bit more work, but maybe it’s worth it?

[alberto]

I added a conclusions section and some more remarks to show how the graphs arising from the unbroken interview are trivial: a pure mathematical artefact.

[alberto]

@Maniamana

Can we perhaps do it both ways, because why not? It is a bit more work, but maybe it’s worth it?

Hmm… I don’t think so. But here is what I would get out of this discussion: a methodological choice that we can put in our “methodology section”, in which we explain why we made the choice we made, and also explain what the consequences of that choice are in terms of induding the network (and, therefore, of interpretation).