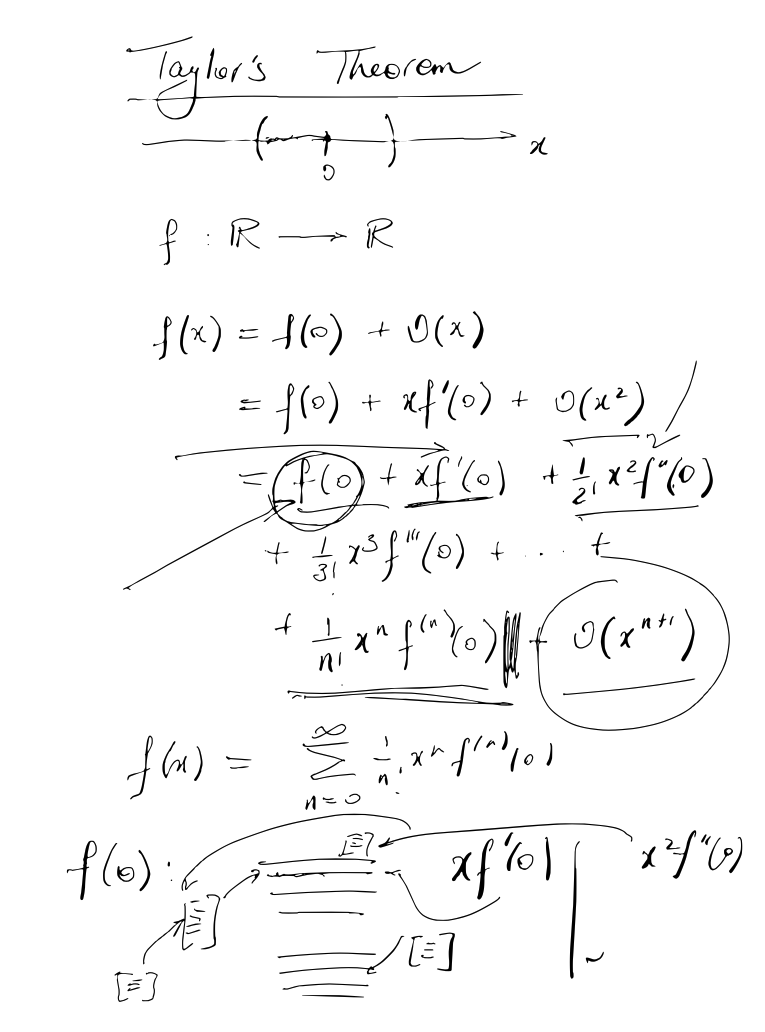I was talking to my partner, Greg, about anthropology yesterday. Greg is a mathematician (his PhD is in mathematical physics). I was lamenting that I did not know when was “enough” in terms of what we call “thick description” in anthropology – what we discussed as “stories” in our white paper meeting the other day, and what we also call “evidence” in our SSNA paper. I said – to capture all the nuances of the situation, there are so many sub-arguments that I want to argue underneath my main argument. But I don’t have room, and no one will read an 10000 page tome (plus, my thesis has a word count limit of 100,000). How much is enough to evidence the argument? And how much detail do I need to take the argument into?
He said this reminded him of Taylor’s Theorem, which he proposed might help me metaphorically. I’ll explain it below in an oversimplified form. 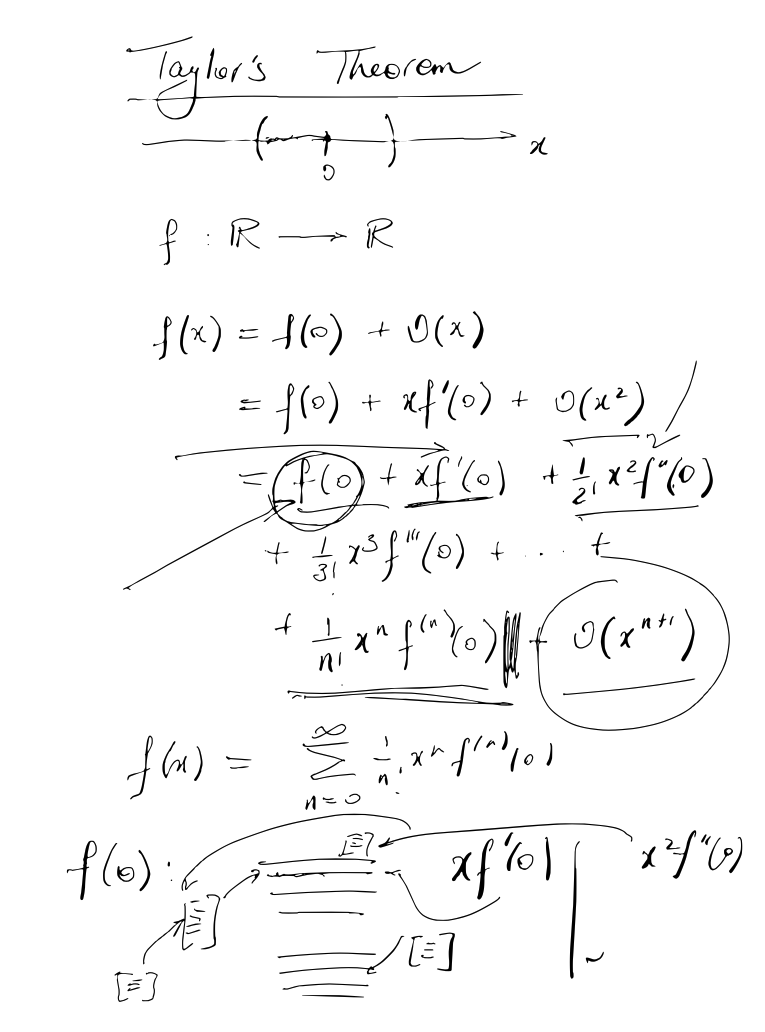
The question he posed: let’s say we have a function, and we don’t know what the function is, but we know it’s very, very complicated. We know for the function, we input a real number and the function spits out another real number for an infinite amount of real numbers. How can we learn about what the function does without having to know every detail of the function itself?
The answer is to start with a zeroth order approximation – in this illustration, f(0). We can take a range of values very close to zero (the range on the number line at the top). And then we have the next term, O(x), which tells us the error. OK, we are not satisfied. Let’s add another approximation, which turns out to be linear, xf’(0). And we keep going until some point at which we feel we have approximated enough and the error is low enough that adding another approximation does not add significantly to our understanding of the function.
He proposed, based upon our conversations about anthropology, to think about it in that way. We make our best first order approximation, and we look at how much of the big complex story (because humans and human behaviour are extremely complex, very contextually determined, etc) is left out when we do that. OK, not good enough. Then we go and add detail to the description we already wrote (this is the diagram at the bottom). Still not good enough. OK, add more. Then we go until the addition of new information or “thickness” doesn’t add significantly to the understanding of the phenomenon we are describing (or until we run out of room).
I think it’s a useful metaphor, and it maps on to the idea of “theoretical saturation” that we have in social sciences, as well. And anthropological writing is always an approximation, because to not approximate we would have to write every detail of the story. The question is – what details are our strongest, most relevant, to explain the phenomenon we have observed?
This doesn’t really answer “how we know what we know”, but it does help explain how we get there and how to explain anthropological knowledge production. (I was also reminded of Bayesian inference a bit, metaphorically, when we discussed this — because it also incorporates the idea that given more information, your explanation of a phenomenon/ability to predict an unknown becomes more accurate in somewhat predictable ways.)